Seitenleiste
Community
Tutorials
Einstieg
Nativ
Web-Programmierung
Fachthemen
mehr...
Inhaltsverzeichnis
Gesamtwiderstand einer Schaltung berechnen
Reihenschaltung
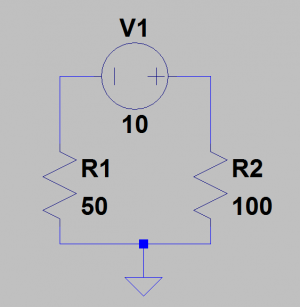
Im Bild sieht man zwei Widerstände die zueinander in Reihe geschaltet sind, d.h. der Strom durchfließt beide Widerstände „nacheinander“. In einer Reihenschaltung addieren sich alle einzelnen Widerstände zu einem Gesamtwiderstand, das obere Bild könnte man nun also durch folgendes Bild auch vereinfach darstellen:
Parallelsschaltung
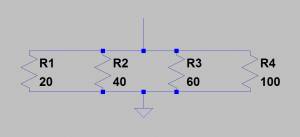
Im oberen Bild sind die Widerstände R1 und R2 parallel geschaltet, d.h. der Strom durchfließt beide Widerstände „gleichzeitig“. Im Gegensatz zur Reihenschaltung addieren sich hier nicht die Widersstandswerte einfach, der Gesamtwiderstand einer Parallelschaltung ist die mathematische Inverse der Summe der Inversen der einzelnen Widerstände (mathematische Inverse von x = 1/x).
oder auch:
In diesem Fall würde also gelten:
Noch ein Beispiel mit etwas mehr Widerständen:
Im Allgemeinen gibt es bei dieser Art von Schaltung noch folgende zwei Sonderfälle, die das Berechnen erleichtern können:
1.Fall: R1=R2
Hier wird es besonders einfach, da der Gesamtwiderstand halb so groß ist wie der Widerstandswert von R1 (oder R2, da R1=R2 gilt). Sind also zwei Widerstände mit jeweils 100 parallel geschalten, beträgt der Gesamtwiderstand der Schaltung 50
.
2. Fall: Nur zwei Widerstände parallel
Dieser Fall trifft auch auf unser obiges Beispiel zu und lässt sich mit folgender Formel leicht lösen: