Seitenleiste
Wiki & Community
User
Moderation
Admin
Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Armin
Steckbrief
| Inhalt | |
|---|---|
| Nick | Armin |
| Name | Armin Böss |
| Beruf | Student |
| Internetseite | Bist gerade drauf ;) |
| Geburtsdatum | 1994 |
| Betriebsysteme | Win7, spiele manchmal mit Linuxsystemenen, aber noch nichts ernstes |
| Werdegang | Erster PC mit 13, mit 14 mit C++, angefangen, danach Python, HTML, CSS, C, und momentan lerne ich etwas Java |
| Über mich | Habe viele Interressen, z.B. Fernöstliche Phylisophie, Kynologie… |
| andere Aktivitäten | Fitness |
Kontaktmöglichkeiten
- PN im Forum
Aktivitäten bei proggen.org
- Arbeite momentan an einem Tutorial für Induktivitäten
Kirchhoffsche Gesetzte
Maschenstromsatz
Der Maschenstromsatz besagt, dass die Summe aller Spannungen innerhalb einer Masche stets Null ist. Doch was bedeutet das genau?
Knotenpunktsatz
Die Summe aller Ströme innerhalb eines Knotens ist stets Null.
Maschenstromverfahren
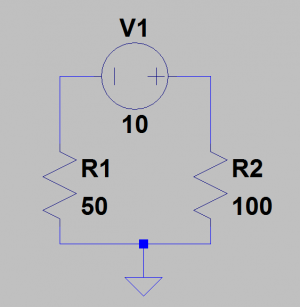
Im oberen Bild sehen wir einen sogenannten Maschenumlauf. Die Pfeile über den Widerständen R1 und R2 deuten die über diese abfallende Spannung an und liefern uns gleichzeitig die „Richtung“ der Spannung. Der „runde“ Pfeil in türkis zeigt uns die vorzeichenrichtige Richtung an, d.h., dass die Spannungen, die in die Richtung fließen, in die der türkise Pfeil zeigt(hier z.B. U(R1)), positiv in die Gleichung eingehen. Zeigt ein Spannungspfeil in die entgegengesetzte Richtung (wie hier z.B. U(V1)), geht diese Spannung mit negativem Vorzeichen in die Gleichung ein. Wie bereits gesagt, besagt der Maschenstromsatz, dass alle Spannungen ein einem Maschenumlauf die Summe 0V ergeben.
Daraus folgt:
Und von obiger Formel wiederum folgt:
Der Großteil der Spannungsberechnungen wäre hiermit abgeschlossen. Um unser Vorhaben zu vollenden, wird nun der Gesamtwiderstand berechnet, aus dem sich dann wiederum der Strom I0 errechnen lässt. Da es sich hier um eine Reihenschaltung von Widerständen handelt, müssen wir, um den Gesamtwiderstand der Schaltung zu ermitteln, lediglich die beiden einzelnen Widerstandswerte addieren.
Aus
folgt, dass
In diesem konkreten Fall:
Da der Strom in einer Reihenschaltung an jeder Stelle (bzw. durch jeden Widerstand) gleich groß ist, kann man nun ganz einfach durch nochmalige Anwenung des Ohm´schen Gesetzes die Spannungen U(R1) und U(R2) errechnen:
⇒
Dazu natürlich noch:
Damit haben wir nun eine Vollständige Analyse des gezeigten Stromkreises durchgeführt.
Wie man sieht, trifft die Anfangsbedingung
voll zu.
Knotensatz
Gesamtwiderstand einer Schaltung berechnen
Reihenschaltung
Im Bild sieht man zwei Widerstände die zueinander in Reihe geschaltet sind, d.h. der Strom durchfließt beide Widerstände „nacheinander“. In einer Reihenschaltung addieren sich alle einzelnen Widerstände zu einem Gesamtwiderstand, das obere Bild könnte man nun also durch folgendes Bild auch vereinfach darstellen:
Parallelsschaltung
Im oberen Bild sind die Widerstände R1 und R2 parallel geschaltet, d.h. der Strom durchfließt beide Widerstände „gleichzeitig“. Im Gegensatz zur Reihenschaltung addieren sich hier nicht die Widersstandswerte einfach, der Gesamtwiderstand einer Parallelschaltung ist die mathematische Inverse der Summe der Inversen der einzelnen Widerstände (mathematische Inverse von x = 1/x).
oder auch:
In diesem Fall würde also gelten:
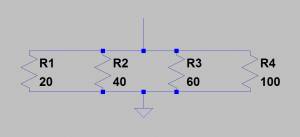
Noch ein Beispiel mit etwas mehr Widerständen:
Im Allgemeinen gibt es bei dieser Art von Schaltung noch folgende zwei Sonderfälle, die das Berechnen erleichtern können:
1.Fall: R1=R2
Hier wird es besonders einfach, da der Gesamtwiderstand halb so groß ist wie der Widerstandswert von R1 (oder R2, da R1=R2 gilt). Sind also zwei Widerstände mit jeweils 100Ω parrallel geschalten, beträgt der Gesamtwiderstand der Schaltung 50Ω.
2. Fall: Nur zwei Widerstände parallel
Dieser Fall trifft auch auf unser obiges Beispiel zu und lässt sich mit folgender Formel leicht lösen:
Elektronikwissen und Elektronikprojekte
Hier soll das Fachgebiet der Elektronik im Analogen sowie Digitalen Bereich näher betrachtet werden.
Dazu wird hier Grundwissen der Elektronik sowie Einsteigerhilfen gegeben, aber auch Projekte Vorgestellt, die die Forumsmitglieder so auf die Beine gestellt haben.